• 何为：最大似然估计（MLE）：

最大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。可以通过采样，获取部分数据，然后通过最大似然估计来获取已知模型的参数。

最大似然估计是一种统计方法，它用来求一个样本集的相关概率密度函数的参数。利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

最大似然估计中采样需满足一个很重要的假设，就是所有的采样都是独立同分布（i.i.d）的。

最大似然估计的一般求解过程：

　　（1） 写出似然函数；

　　（2） 对似然函数取对数，并整理；

　　（3） 求导数 ；

　　（4） 解似然方程。

 

• 何为：最大后验概率（MAP）：

最大后验估计是根据经验数据获得对难以观察的量的点估计。

与最大似然估计类似，但是最大的不同是，最大后验估计融入了要估计量的先验分布在其中。

故最大后验估计可以看做规则化的最大似然估计。

 

• 什么情况下，MAP=ML？

当模型的参数本身的概率是均匀的，即该概率为一个固定值的时候，二者相等。

 

当先验分布均匀之时，MAP 估计与 MLE 相等。下图是均匀分布的一个实例。

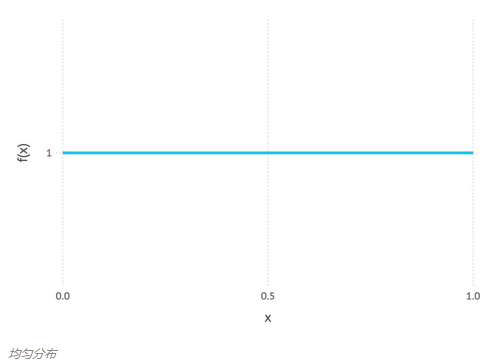
我们可以看到均匀分布给 X 轴（水平线）上的每个值分布相同的权重。直观讲，它表征了最有可能值的任何先验知识的匮乏。在这一情况中，所有权重分配到似然函数，因此当我们把先验与似然相乘，由此得到的后验极其类似于似然。因此，最大似然方法可被看作一种特殊的 MAP。

 

【Reference】

[1] 

[2]